Template:Table/Template:InheritValueTable

This template contains swapped content from page Template:InheritValueTable

Why is this necessary?

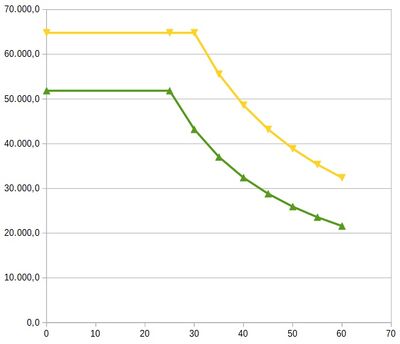
This is an example for usage of <valueTable> with a series of two curves (force vs. speed) which are differentiated by a constant power limitation.

		Speed  Force100  Force66.7 0 64.800,9 51.840,0 25 64.800,9 51.840,0 30 64.800,9 43.200,0 35 55.542,9 37.028,6 40 48.600,0 32.400,0 45 43.200,0 28.800,0 50 38.880,0 25.920,0 55 35.345,5 23.563,6 60 32.400,0 21.600,0
Graphical representation of the curves.		The value table in a spreadsheet.

railML^®-Code

<valueTable yValueUnit="N" xValueName="speed" yValueName="tractive effort" 
	xValueUnit="km/h" zValueName="Percentage power limitation" zValueUnit="%">
	<columnHeader zValue="100" /><columnHeader zValue="66.7" />
	<valueLine xValue="0.0">
		<values yValue="64800" /><values yValue="51840" />
	</valueLine>
	<valueLine xValue="25.0">
		<values yValue="64800" /><values yValue="51840" />
	</valueLine>
	<valueLine xValue="30.0">
		<values yValue="64800" /><values yValue="43200" />
	</valueLine>
	<valueLine xValue="35.0">
		<values yValue="55542.9" /><values yValue="37028.6" />
	</valueLine>
	<valueLine xValue="40.0">
		<values yValue="48600" /><values yValue="32400" />
	</valueLine>
	<valueLine xValue="45.0">
		<values yValue="43200" /><values yValue="28800" />
	</valueLine>
	<valueLine xValue="50.0">
		<values yValue="38880" /><values yValue="25920" />
	</valueLine>
	<valueLine xValue="55.0">
		<values yValue="35345.5" /><values yValue="23563.6" />
	</valueLine>
	<valueLine xValue="60.0">
		<values yValue="32400" /><values yValue="21600" />
	</valueLine>
</valueTable>

When using the <valueTable> as representation of a series of curves (three-dimensional function) it shall be written in railML^® similar as in a spreadsheet. It means first the header has to be defined with the value descriptions. Second the particular z-values valid for each curve out of the series are to be listed as child element <columnHeader>. Finally the respective <valueLine> for each x-value of the curves is included. Per each x-value there must be as much y-values as the number of curves (number of z-values). The order of y-values is according the order of z-values. Thus a clear assignment to the related curve is made. It shall be noted that the x-values may be not equidistant. In case the original series of curves have different x-values then interpolation must be used to get the missing y-values per each x-value occurring in the series.